Constraining Neural Network activations with Partial Differential Equations
Introduction
Recently I came across an interesting paper: Condensing CNNs with Partial Differential Equations by Kag et al. The paper proposes a way to enforce constraints on the intermediate activations in a CNN model. What is the advantage of enforcing these constraints ? Through extensive experiments on different datasets [ImageNet included] they show that it’s possible to reduce the computational and storage costs by 2-5 times without any significant loss in performance! Their proposed layer which applies PDE constraints is also easy to incorporate into existing CNN architectures. The author’s provide PyTorch code to replicate their experiments. I have reproduced their main results in TensorFlow. The code is here.
Diffusion-Advection PDE
In the 2D case, the Diffusion-Advection PDE is as follows: \begin{equation} \frac{\partial H(x, y, t)}{\partial t} + \frac{\partial u(x,y,t) H(x, y, t)}{\partial x} + \frac{\partial v(x,y,t) H(x, y, t)}{\partial y} = \\ \frac{\partial D_x H(x, y, t)}{\partial x} + \frac{\partial D_y H(x, y, t)}{\partial y} + f(I(x,y)) \end{equation} $D_x$ and $D_y$ are the diffusion coefficients, $u$ and $v$ are the velocity coefficients. $f(I(x,y))$ is the source of $H$. $H(x,y,t)$ is the CNN feature map that we wish to constrain using the diffusion-advection PDE. It can be noticed that $H(x,y,t)$ is dependant on x, y and $t$. The dependence on $x,y$ is obvious since the feature maps obviously vary spatially. The activation map also varies with time. In the implementation the time dependance corresponds to the number of iterations.
The above equation is in continuous space and time. Hence for a practical implementation we need to discretise it. Assuming a certain discrete step size, it is possible to expand the PDE operators. The calculation is tedious but straight-forward. Upon discretisation we get the following equation: \begin{equation} L H_{x,y}^{k+1} = M H_{x,y}^{k-1} - 2(u_x + v_y) \delta_t H_{x,y}^{k} + 2 \delta_t f(I(x,y)) \\ + (-A_x + 2B_x)H_{x+1,y}^{k} + (A_x + 2B_x) H_{x-1,y}^{k} + \\ (-A_y + 2 B_y)H_{x,y+1}^{k} + (A_y + 2 B_y) H_{x,y-1}^{k} \end{equation}
where $L = (1+2B_x + 2B_y)$ and $M = (1-2B_x - 2B_y)$ $u_x$, $v_y$ are approximated using central difference on velocities $u$ and $v$. $A_x = \frac{u \delta_t}{\delta_x}$, $A_y = \frac{v \delta_t}{\delta_y}$, $B_x = \frac{D_x \delta_t}{\delta_x^2}$, $B_y = \frac{D_y \delta_t}{\delta_y^2}$
Although the above equation looks complicated it is not too difficult to implement in practice. For implementation, we also need a few more details namely the function f, particle velocity [u, v], and diffusion coefficients [$D_x$ , $D_y$]. The paper studies the impact of different choices for the above parameters in the ablation study. Generally we use an identity function as f whereas $u,v,D_x,D_y$ are learnt during model training.
Experiments with MNIST
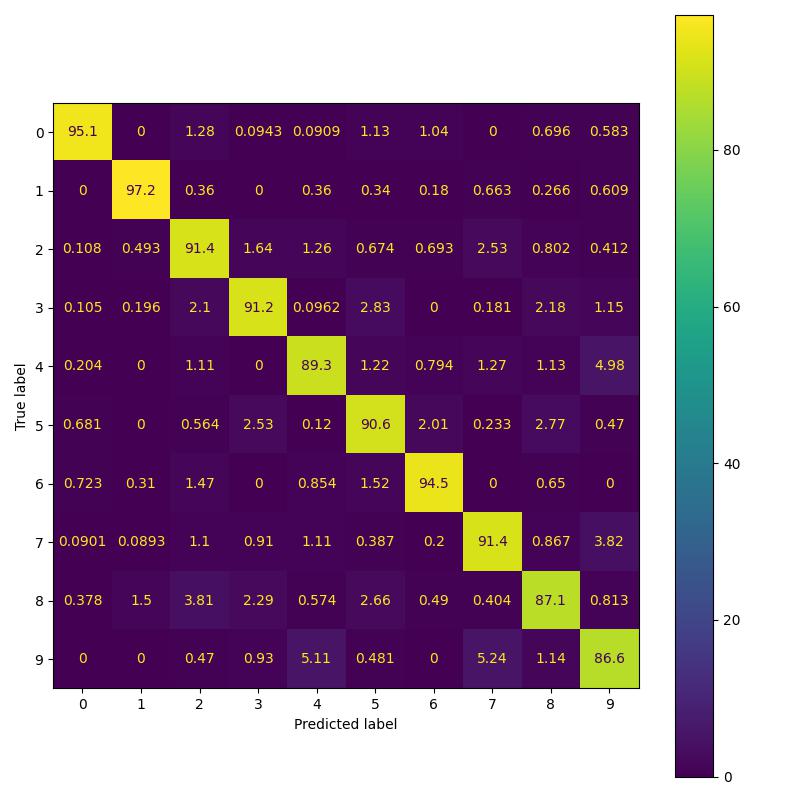
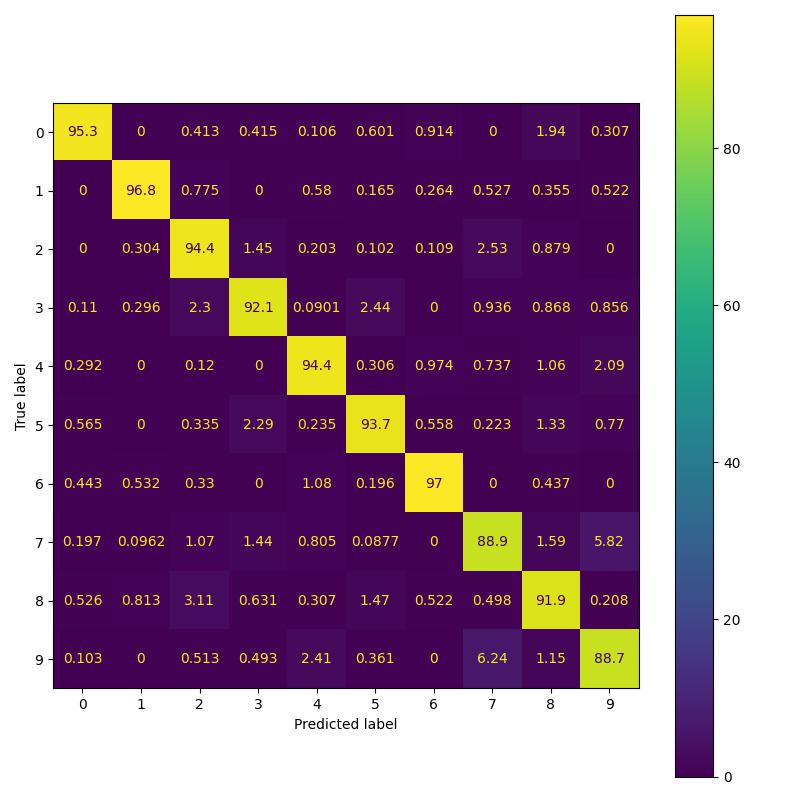
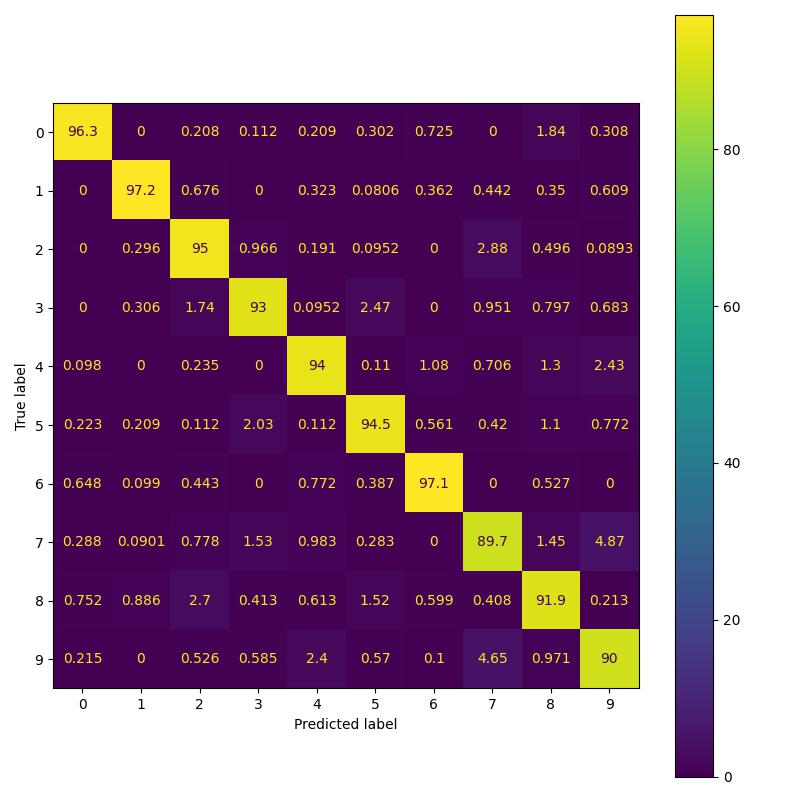
To replicate the results in Table 2 of the paper, I implemented three variants namely: simple CNN model, residual model and PDE model. As per the paper all three models should have 524 parameters. However I observed that the CNN model as implemented in their Pytorch repo has 522 parameters instead of 524 parameters. This issue has been brought to the author’s attention. For the purpose of replicating results, I perform a comparison of residual and pde model having 524 parameters with CNN model having 522 parameters [following paper’s pytorch implementation].
| Feature Backbone | Paper Acc. (%) | Our Acc. (%) | Confusion b/w 3 and 5 (%) |
|---|---|---|---|
| Convolution | 92.01 | 91.5 | 2.53 |
| Residual | 92.53 | 93.39 | 2.29 |
| Global | 95.03 | 93.96 | 2.03 |
Replicating MNIST results of the paper.
Replicating CIFAR-10 results
For the purpose of replicating the paper’s result from Table 3, rows 7-8, I re-implemented their architecture in Tensorflow. I used the paper’s proposed setting for hyperparameters like learning rate and weight decay. Choice of optimizer, augmentation scheme and input normalization was also fixed according to the paper. I ran the experiments 3 times and noticed slight differences in test accuracy (+/-0.5%). I report the best obtained accuracy across different runs in Table 2. There is a slight difference in accuracy score between our implementation and the paper results. This could be explained by difference in implementation of SGD with momentum optimizer in PyTorch and Tensorflow [@SGDPytorch1] [@SGDPytorch2].
| Feature Backbone | Paper Acc. (%) | Our Acc. (%) | Parameters |
|---|---|---|---|
| Resnet32 | 92.53 | 90.9 | 460K |
| Global (K=1) | 91.93 | 88.59 | 162K |
Comparison of Resnet 32 and Global (K=1) model on CIFAR 10 test set.
Visualization of the parameters of diffusion-advection PDE
Visualizing Dx for the three global PDE layers

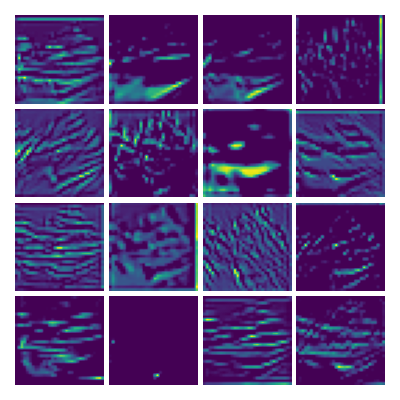
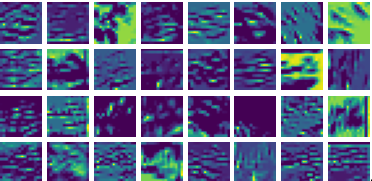

Visualizing Dy for the three global PDE layers

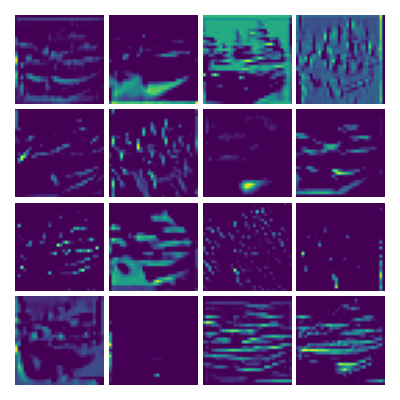

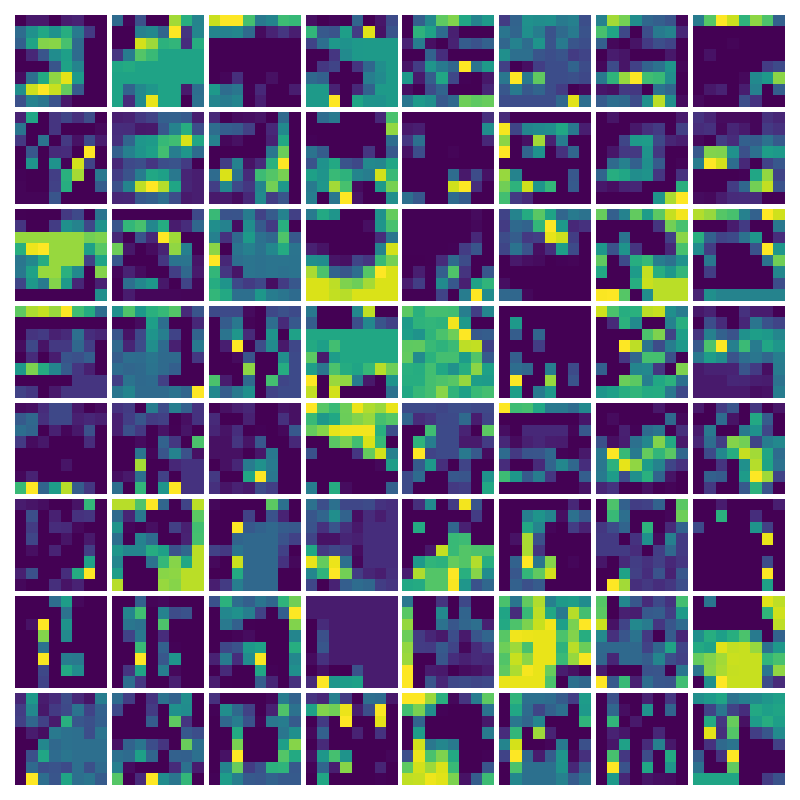
Visualizing g for the three global PDE layers



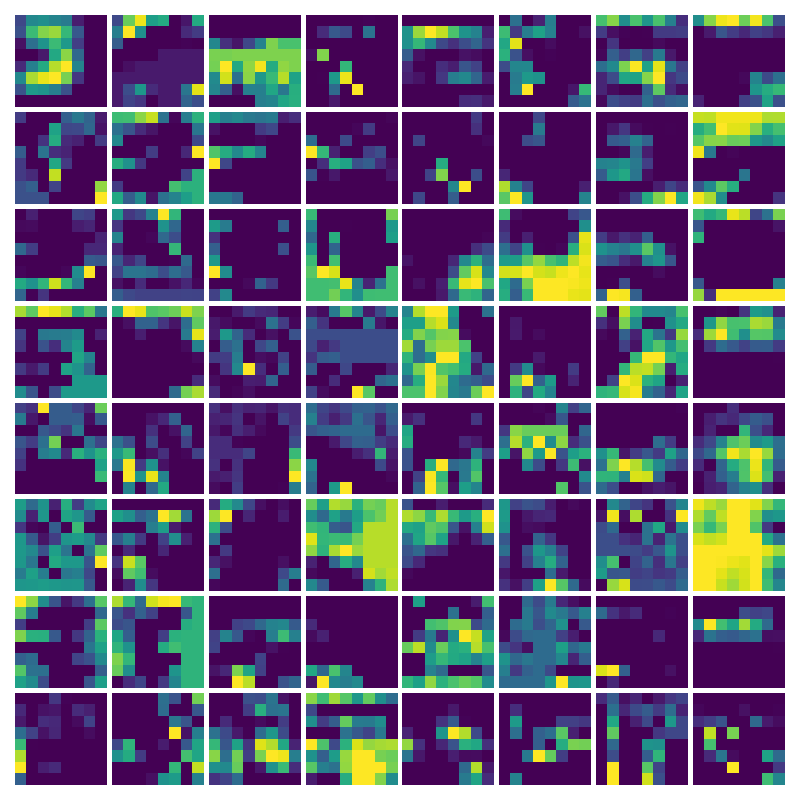
Visualizing g1 for the three global PDE layers



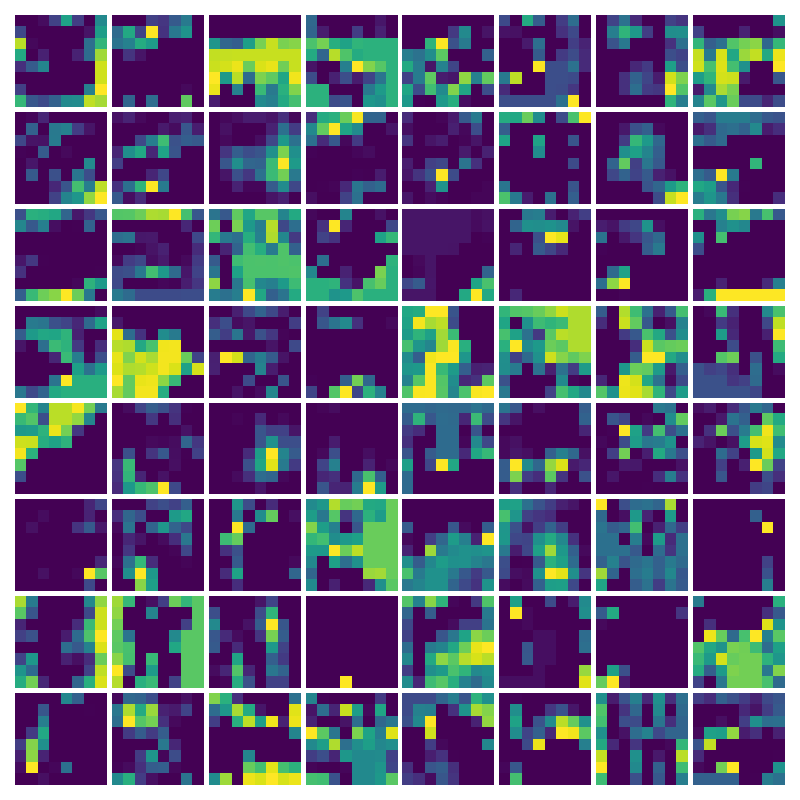
Visualizing ux for the three global PDE layers



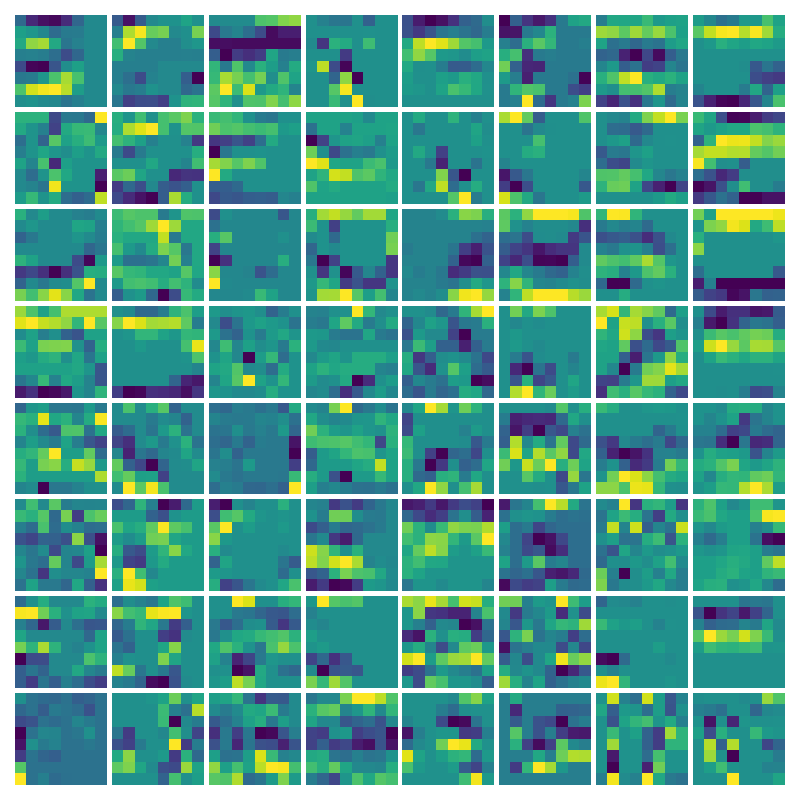
Visualizing vy for the three global PDE layers


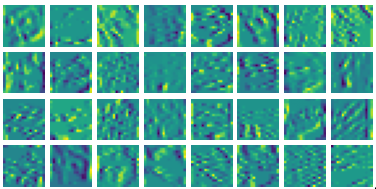
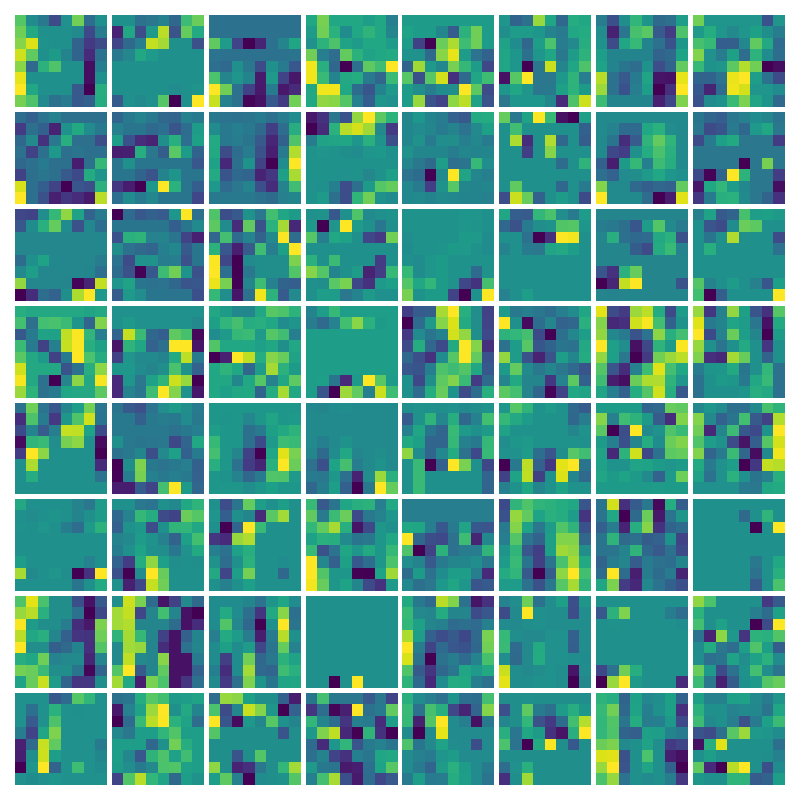
Ablation study
| Method | Acc. (%) | Parameters |
|---|---|---|
| Baseline | 90.9 | 460K |
| Global (K=1) | 88.64 | 162K |
| Constant Dxy (K=1) | 88.60 | 159K |
| No Advection (K=1) | 87.86 | 159K |
| No Diffusion (K=1) | 88.03 | 159K |
Ablation results on CIFAR-10 test set.
Based on the ablation study we can observe the following:
-
It is not necessary to parameterize and learn the diffusion part. Setting reasonable default values for the diffusion coefficients $D_x$ and $D_y$ gives good results.
-
Disabling advection or diffusion parts of PDE reduced the test accuracy slightly.
References:
Kag, Anil and Saligrama, Venkatesh Condensing CNNs With Partial
Differential Equations, Proceedings of the IEEE/CVF Conference on
Computer Vision and Pattern Recognition (CVPR)
Siddhartha, Possible bug in mnist illustrative example,
https://github.com/anilkagak2/PDE_GlobalLayer/issues/1.
Lee Ceshine, SGD implementation in PyTorch,
https://medium.com/the-artificial-impostor/sgd-implementation-in-pytorch-4115bcb9f02c.
Thomas V Different SGD implementation in PyTorch,
https://discuss.pytorch.org/t/sgd-with-momentum-why-the-formula-change/135444/2.
